円と円の当たり判定をやります。
円と円の当たり判定では、四角形より少し難しいです、でも少しだけです。
では、下の図を見てください

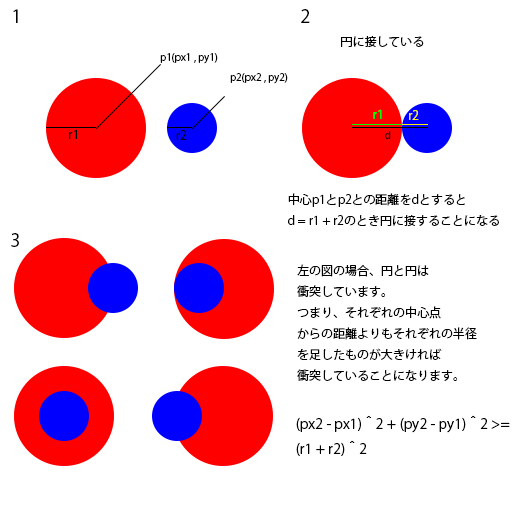
1.赤、青の二つの円があり、それぞれp1,p2とします。
また、赤円の中心をp1(px1,py1),青円の中心をp2(qx1,qy2)とします。

円と円が接する場合、図でわかるように中心p1とp2の距離をdとすると、
d = r1 + r2の場合に接することになります。

今回必要な、円の中心と円の中心との距離を求めるためには、
三平方の定理が必要になります。↓を見てください

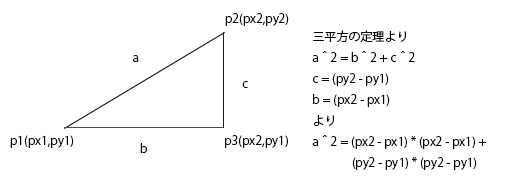
p1,p2をそれぞれ、円の中心だとすると、円の中心間の距離dは
d^2 = (px2 - px1) × (py2 - py1)
とういうことになります。

では、最後に円と円との当たり判定です。
図でわかるように、円と円との中心座標の距離がよりも両方の半径が長ければ
円と円が衝突していることになります。
これをコードで表すと

if((px2 - px1) * (px2 - px1) + (py2 - py1) * (py2 - py1) <= (r1 + r2) * (r1 + r2))
{
	// 円と円が衝突
}
		

上記のコードでは、ルート演算であるsqrtを使用して、計算することもできますが
sqrtを使用すると、上記の演算よりも遅くなってしまうので、使用しませんでした。

今回、ブラウザ上でのサンプルを作るにあたって、マウスで円をドラックさせる処理を作ったので
円と点の当たり判定も使用しました。
当たり前ですが、点と円の中心との距離が半径よりも短ければ衝突しています。
点の座標をp(px,py),円の中心をc(cx,cy),半径をrとします。

if((cx - px) * (cx - px) + (cy - py) * (cy - py) <= r * r)
{
	// 点と円とが衝突
}
		

お疲れ様でした。

今回のサンプル