線分と円との当たり判定です。
線との違いは、線上に存在する最短点が必ずしも存在しないことです。
当たり判定では、当たっていると見なされる2つの可能性があります。

一つ目は、2つの線分の端点が円の内部に存在するかどうか。
二つ目は、線分の端点が円の内部に存在せず、線分が円をまたがっている状態をさします。

それでは、図で確認してみます。

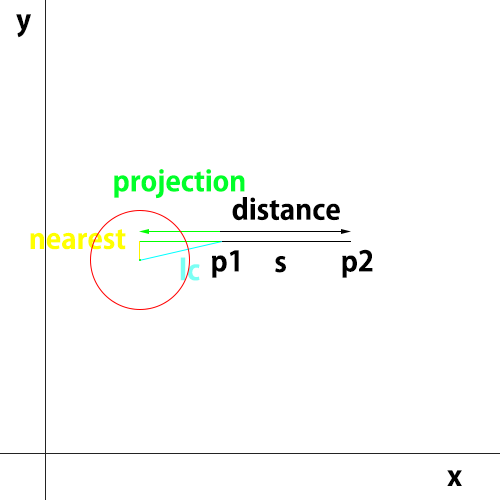
線分sがあり円との当たり判定の関係をみていきます。
射影ベクトルがprojection
点であるnearestは線分pが線である場合の最短点を表します。

当たり判定では、上記で述べた2点をチェックします。
まず、2つの線分の端点が円の内部に存在しないことをチェックすることで
線分が円にまたがっている場合のみのケースに限定します。

// segmentの端点がサークル内に存在するか
if(circle.CollisionWithPoint(segment.point1) || circle.CollisionWithPoint(segment.point2)){
	return true;
}
		

残りは、線分が円にまたがって存在しているかどうかをチェックすればいいことになります。
線分が円にまたがって存在しているかどうかをチェックするには、以下の要素をチェックします。

近接点が円内部に存在する

線分の長さが円の中心から線分の端点へのベクトルと線分との射影ベクトルの長さ以上である

線分と射影ベクトルの内積が-である。

これらの三つの要素が成り立つ場合線分が円にまたがっていることになります。

文字だけだと理解しにくいので、サンプルを作成してみました。
黒線分が対象となる線分s
赤が射影ベクトルprojection
黄色が線分の端点と円の中心を結んだ線分lc
緑の線分が近接点であるnearestと円の中心点を結んだ線分です

ドラッグすることで、線分を動かせるので、各々の条件を確認してみてください。

内積がマイナスになるときは、対象のベクトルのなす角が90度以上であることです。

なぜ3つの条件が重なると、当たっていることになるのか、図で確認してみます。

以下の場面は
最短点が円の内部にあり、線分ベクトルが、射影ベクトルよりも長いが、内積の条件を満たしていません。

また、以下の場面は、最短点が内部にあり、内積の条件を満たしていますが、線分の長さが射影ベクトルの長さより小さいので、
条件を満たしていません。

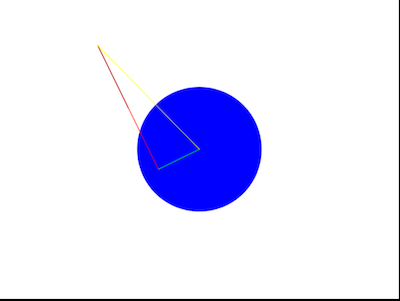
以上より、3つのケースのかつ条件チェックをする必要があることがわかります。
最後にコードを載せておきます

/**
	chapter7

	circle = cCircle
	segment = LineSegment2D

*/
function collision_circle_with_segment(circle,segment){
	// segmentの端点がサークル内に存在するか
	if(circle.CollisionWithPoint(segment.point1) || circle.CollisionWithPoint(segment.point2)){
		return true;
	}
	// segmentをベクトルに変換
	var distance = subtractVector(segment.point2,segment.point1);
	// point1から円の中心へのベクトルを求める
	var lc = subtractVector(circle.Center,segment.point1);
	// lcとsegmentとの射影ベクトルを求める
	var project = projectVector(lc,distance);

	// 取得した射影ベクトルとの近接点を求める
	var nearest = getAddVector(segment.point1,project);
	// 近接点が円内部に存在するかつ線分の長さが射影ベクトルの長さ以上かつ線分と射影ベクトルの内積が-である
	return circle.CollisionWithPoint(nearest) && getVectorLength2D(project) <= getVectorLength2D(distance)
	 && 0 <= dotProduct2D(project,distance);
}