正射影ベクトルに関してみていきます
英語でいうところのProductionVectorです
どのような概念なのか？図で見て見ます。

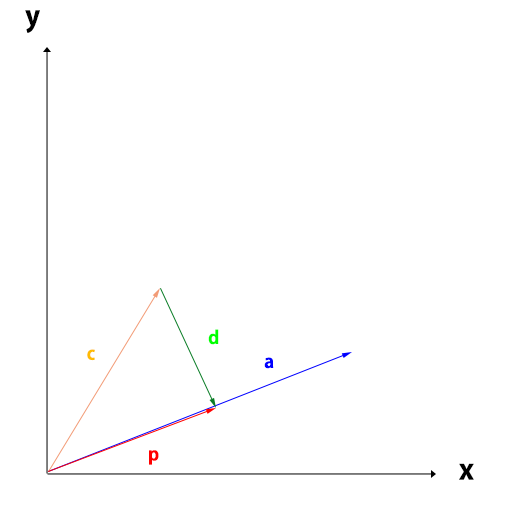
赤色で表示されているベクトルaとベクトルcの正射影ベクトルになります。
図でみてわかるように、正射影ベクトルpはcベクトルからaベクトルに垂直に下ろしたベクトルdの端点になっています。 では、正射影ベクトルpをjavascriptで関数化してみます。

function projectVector(project,onto)
	// 内積を使って長さを求める
	float d = dotProduct(onto,onto);
	
	if(0 < d){
		float dp = dotProduct(project,onto);
		
		return multiply_vector(onto,dp / d);
	}
	return onto;
}
		

これを解析しましょう。
図に添って見ていきます。

        (1)ベクトルaとベクトルcのなす角をαとすると、
        三角関数より、
        cos(α) = length(p) / length(b)
        
        (2)内積の定義により
        cos(α) * length(v1) * length(v2) = dotProduct(v1,v2);
        より、
        
        (3)これを図に当てはめると
        cos(α) * length(a) * length(b) = dotProduct(a,b);
        
        (4)
        (1)(3)を用いて、cos(α)入れ替えて、
        
        (length(p) / length(b)) * length(a) * length(b) = dotProduct(a,b);
        
        (5).(4)を計算し、length(b)を消去して、
        
        length(p) = dotProduct(a,b) / length(a);
        
        (6)単位ベクトルpと単位ベクトルaは同じベクトルであるから、
        unitVector(p) = unitVector(a) = p / length(p);
        
        (7)また、ベクトルpは以下のようにも表すことができる
        p = unitVector(a) * length(p);
        
        (8).(7),(5)を用いて、以下のように表すことができる
        p = unitVector(a) * dotProduct(a,b) / length(a);
        
        (10).(8)のunitVectorを計算して
	p = (a / length(a)) * (dotProduct(a,b) / length(a));
		
	(11)これを計算して
	p = a * dotProduct(a,b) / length(a) * length(a)
		
	(12)length(a)を内積に置き換えて
	p = a * dotProduct(a,b) / dotProduct(a,a)        
        

これで、関数で使われている演算結果が求められました。

図において、正射影ベクトルの概念と、プログラムにおいて、求め方を学びました