気体の圧力の求め方と単位変換

気体の圧力の求め方、考え方についてまとめます。

単位面積あたりに加わる力のことを圧力といいます。

力の大きさを$[N]$、力を受ける面積を$[m^2]$とすると圧力は

圧力$[N/m^2]$ = 力の大きさ[N] ÷ 力を受ける面積$[m^2]$

大気圧(空気の圧力)は昔、水銀を用いて求めようとされたため入試でも水銀量で出題されることがあります。

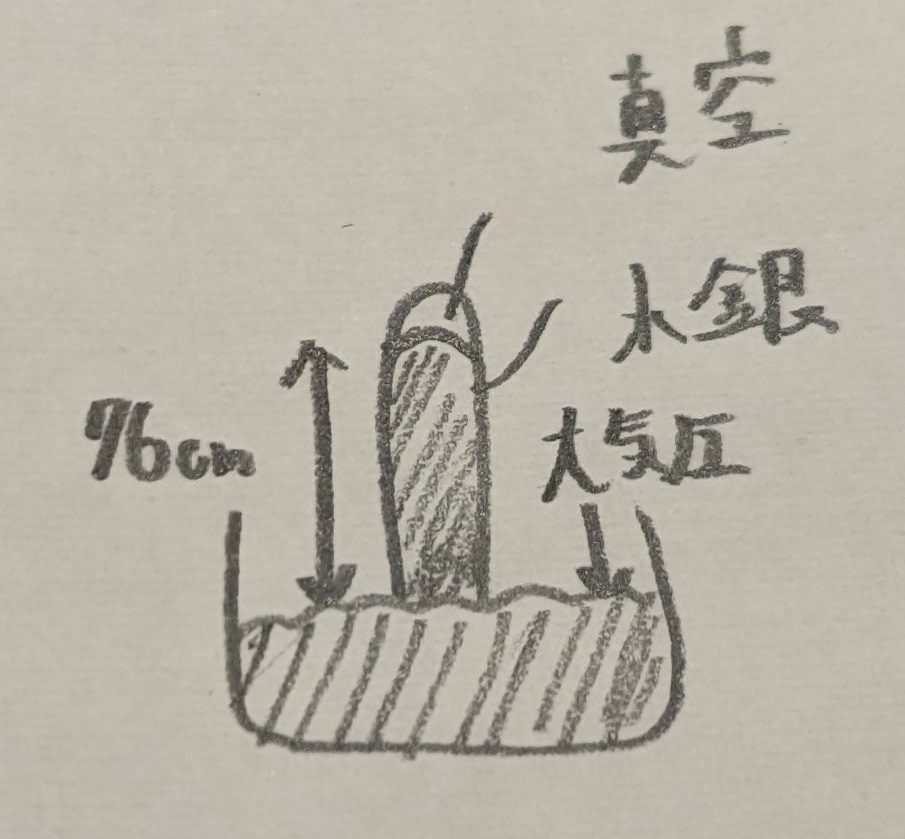
下図のように水銀を真空のガラス管の中入れてひっくり返すと、76cmのところで止まるので、
大気圧を水銀量76cmと表現します。

よって、1気圧は水銀で表すと

$1atm(1気圧) = 76cmHg = 760mmHg$

通常$mm$を使って表現することが多いです。

先の図の水銀柱の底面積を$S[cm^2]$とすると、水銀の体積Vは底面積×高さで表されるので

$V = S[cm^2] \times 76[cm] = 76S[cm^3]$

水銀の密度は$13.6[g/cm^3]$なので、水銀の質量は

$76S[cm^3] \times \dfrac{13.6g}{1[cm^3]} = 1033.6S[g]$

ここで、1kgの物体に働く重力が$9.8[N]$と圧力の定義を用いると、
水銀柱の底面に働いている圧力$P$は

$P = \left \{ 1033.6S[g] \times \dfrac{1[kg]}{10^3[g]} \times \dfrac{9.8[N]}{1[kg]} \right \} \div \left \{ S[cm^2] \times \left( \dfrac{1[m]}{10^2[cm]} \right)^2 \right \}$

単位を相殺すると

$ = \dfrac{ 1033.6S \times 10^{-3} \times 9.8[N]}{S \times 10^{-4}[m^2]} \fallingdotseq 1.01 \times 10^5[N/m^2]$

$1[Pa] = 1[N/m^2]$より

$1.01 \times 10^5[N/m^2] = 1.01 \times 10^5[Pa]$

これらをまとめると

$1atm = 760mmHg = 1.01 \times 10^5 N/m^2 = 1.01 \times 10^5[Pa]$

初版:2024/1/20

Tweet