共分散と相関係数について

共分散と相関係数についてまとめます。

共分散$S_{xy}$

$x$の偏差と$y$の偏差の積$(x_k - \overline{x})(y_k - \overline{y})$の平均値のこと

$S_{xy} = \dfrac{1}{n}\{(x_1 - \overline{x})(y_1 - \overline{y}) + (x_2 - \overline{x})(y_2 - \overline{y}) + ・・・ + (x_n - \overline{x})(y_n - \overline{y})\}$

共分散$S_{xy} > 0$のとき、下図の「+」部分にある

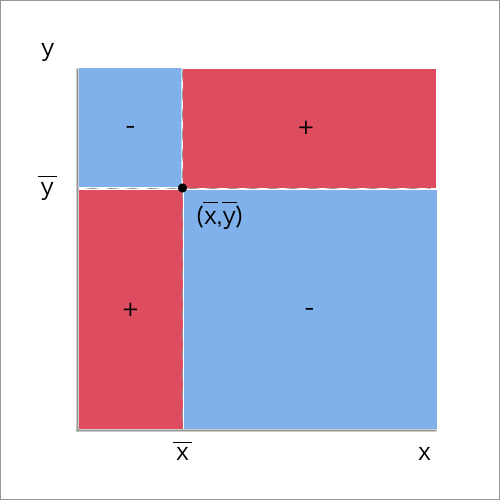
点$(x_k,y_k)が多い$ → 正の相関関係がある。

共分散$S_{xy} < 0$のとき、上図の「-」部分にある

点$(x_k,y_k)が多い$ → 負の相関関係がある。

相関関係の強弱を見る指標のこと

$x$、$y$の標準偏差をそれぞれ、$s_x,s_y$とするとき

$r = \dfrac{s_{xy}}{s_xs_y} = \dfrac{(x_1 - \overline{x})(y_1 - \overline{y}) + \cdot \cdot \cdot + (x_n - \overline{x})(y_n - \overline{y})}{\sqrt{\{(x_1 - \overline{x})^2 + \cdot \cdot \cdot + (x_n - \overline{x})^2\}\{(y_1 - \overline{y})^2 + \cdot \cdot \cdot + (y_n - \overline{y})^2\}}}$

相関関数$r$は$-1 \leqq r \leqq 1$で

$r > 0 \Leftrightarrow\ s_{xy} > 0$

$r < 0 \Leftrightarrow\ s_{xy} < 0$

また、

1.$r$の値が1に近い時、強い正の相関関係がある

2.$r$の値が-1に近い時、強い負の相関関係がある。

3.$r$の値が0に近い時、直接的な相関関係はない。

初版:2021/8/25