チェバの定理の逆

三角形ABCの辺BC,CA,ABまたはその延長上に、それぞれ点D,E,Fをとる。
この3点のうち、辺の延長上にある点の個数は0か2であるとする。

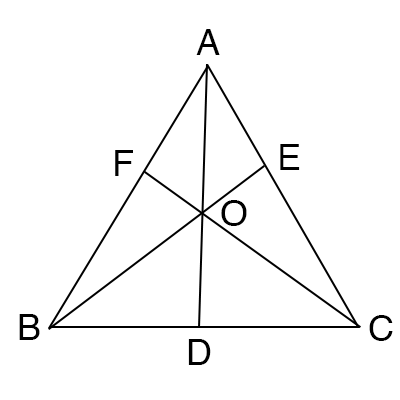
このとき、BEとCFが交わる。

かつ、\(\frac{BD}{DC} \cdot \frac{CE}{EA} \cdot \frac{AF}{FB} = 1 \)

が成り立てば、AD,BE,CFは一点で交わる。

これをチェバの定理逆といいます。

下図のように、点D,Eがともに辺上にあるか、またはともに辺の延長上にあるものとすると、
点Eは辺AC上の点である。

2直線AD,CFの交点をOとすると、Oは2直線BA,BCによってできる\(\angle ABC\)またはその対頂角の内部にあるから、
直線BOは辺ACと交わる。

その交点をE'とすると、チェバの定理により

$$\frac{BD}{DC} \cdot \frac{CE'}{E'A} \cdot \frac{AF}{FB} = 1$$

これと、条件の等式より

\(\frac{CE'}{E'A} = \frac{CE}{EA}\)

E、E'はともに辺BC上にあるから、E'はEと一致する。

したがって、3直線AD,BE,CFは一点で交わる。

初版:2021/6/22

Tweet