内分点と外分点の座標を求める公式とその証明について

2点$A(a),B(b)$を$m:n$に内分する点の座標は

$\dfrac{na + mb}{m + n}$

2点$A(a),B(b)$を$m:n$に外分する点の座標は

$\dfrac{-na + mb}{m - n}$

内分・外分する点を$P$とします。
まず、下図のように点$A$と$B$を$m:n$に内分する点$P(x)$の座標を考えます。

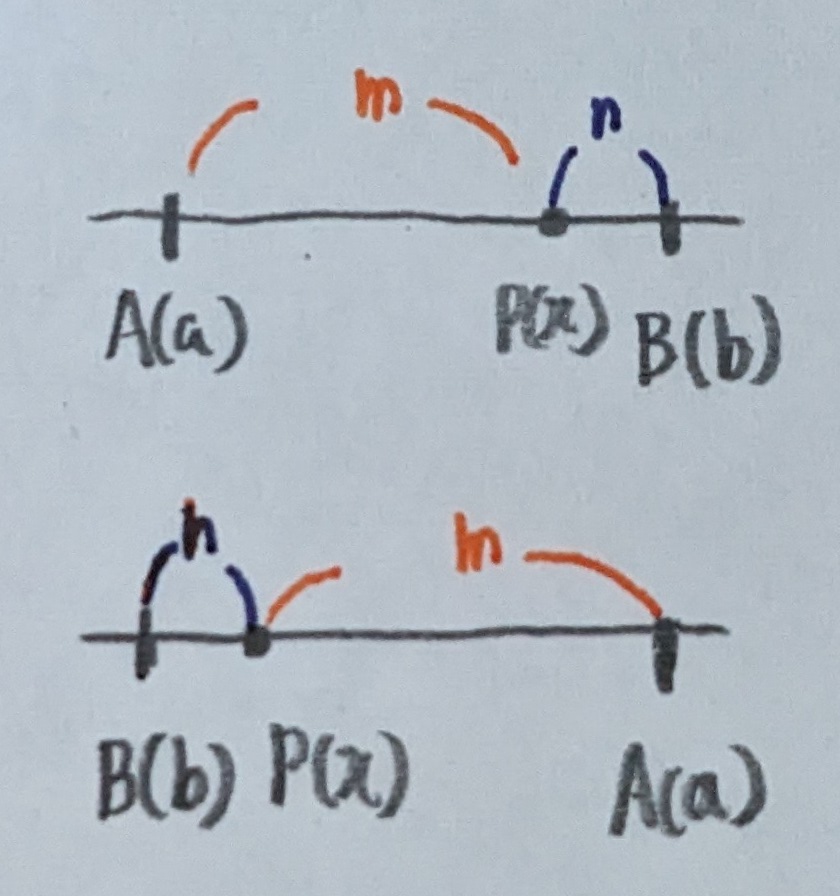
$AP:PB = m : n$より

$|x - a| : |b - x| = m : n$

$n|x - a| = m|b - x| - ①$

上図より$x - a$と$b - x$は同符号になるので、

$n(x - a) = m(b - x)$

これを$x$について解くと

$x = \dfrac{na + mb}{m + n}$

次に、下図のように点$A$と$B$を$m:n$に外分する点$P(x)$の座標を考えます。

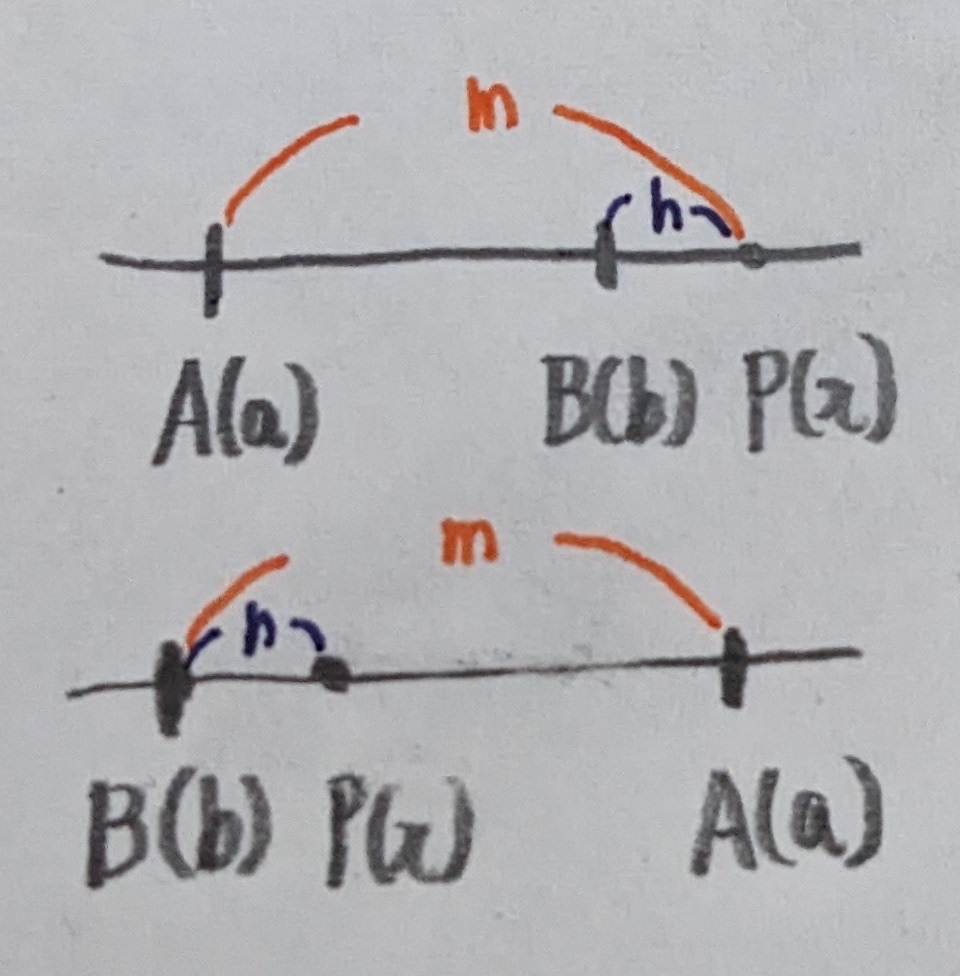
上図より、$AP:PB = m : n$より内分点と同様に$①$の式が得られます。

また、上図より

$x - a$と$b - x$は異符号になるので

$-n(x - a) = m(b - x)$

これを$x$について解くと

$x = \dfrac{-na + mb}{m - n}$

初版:2024/1/11

Tweet