電機振動と関連する公式

コンデンサーにコイルがつながっている様な回路を振動回路と呼びます。

この様な回路でコンデンサーを充電しコイルをつなぐと、コンデンサーに蓄えられる電気量と回路に流れる電流が一定の周期で変化します。
この現象を電気振動といいます。

電気振動ではコンデンサーに蓄えられる静電エネルギーとコイルに蓄えられるエネルギーの和が一定になります。
よって、次の等式が成り立ちます。

$$\displaystyle \frac{1}{2}LI^2 + \frac{Q^2}{2C} = 一定$$

電気振動の周期は共振周波数と同じで、

$$\displaystyle T = 2π \sqrt{LC}[Hz]$$

コイルの自己インダクタンスを$L$、コンデンサーの電気容量をCとすると、
下図の電気泳動を考えて、

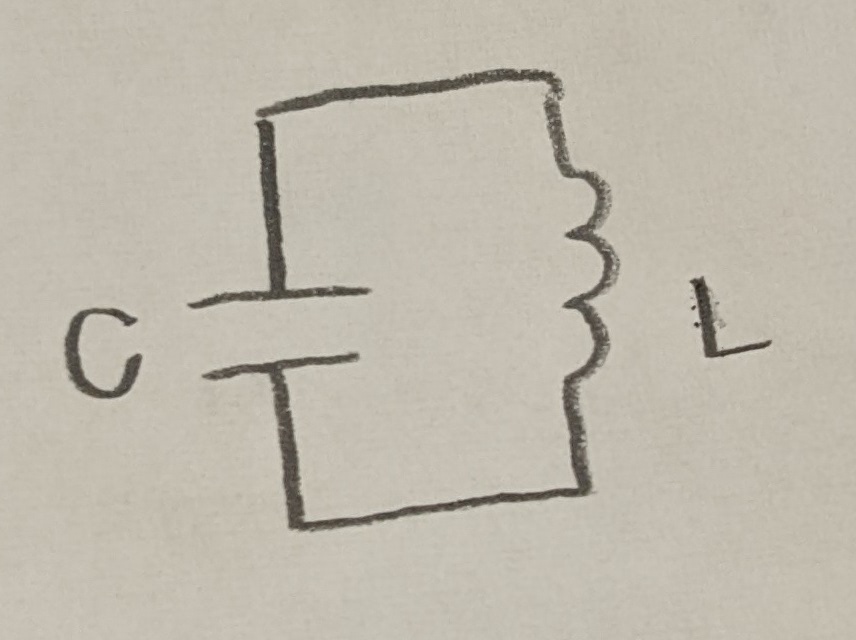
キルヒホッフより

$V_L = V_C$

流れる電流を$I$として

$ωLI = \dfrac{1}{ωC}I$

$ω^2 = \dfrac{1}{LC}$

$ω = \dfrac{1}{\sqrt{LC}}$

$T = \dfrac{2π}{ω} = 2π\sqrt{LC}$

初版:2022/9/10
更新:2023/12/24(電気泳動の証明を追加)